*******************************************************************
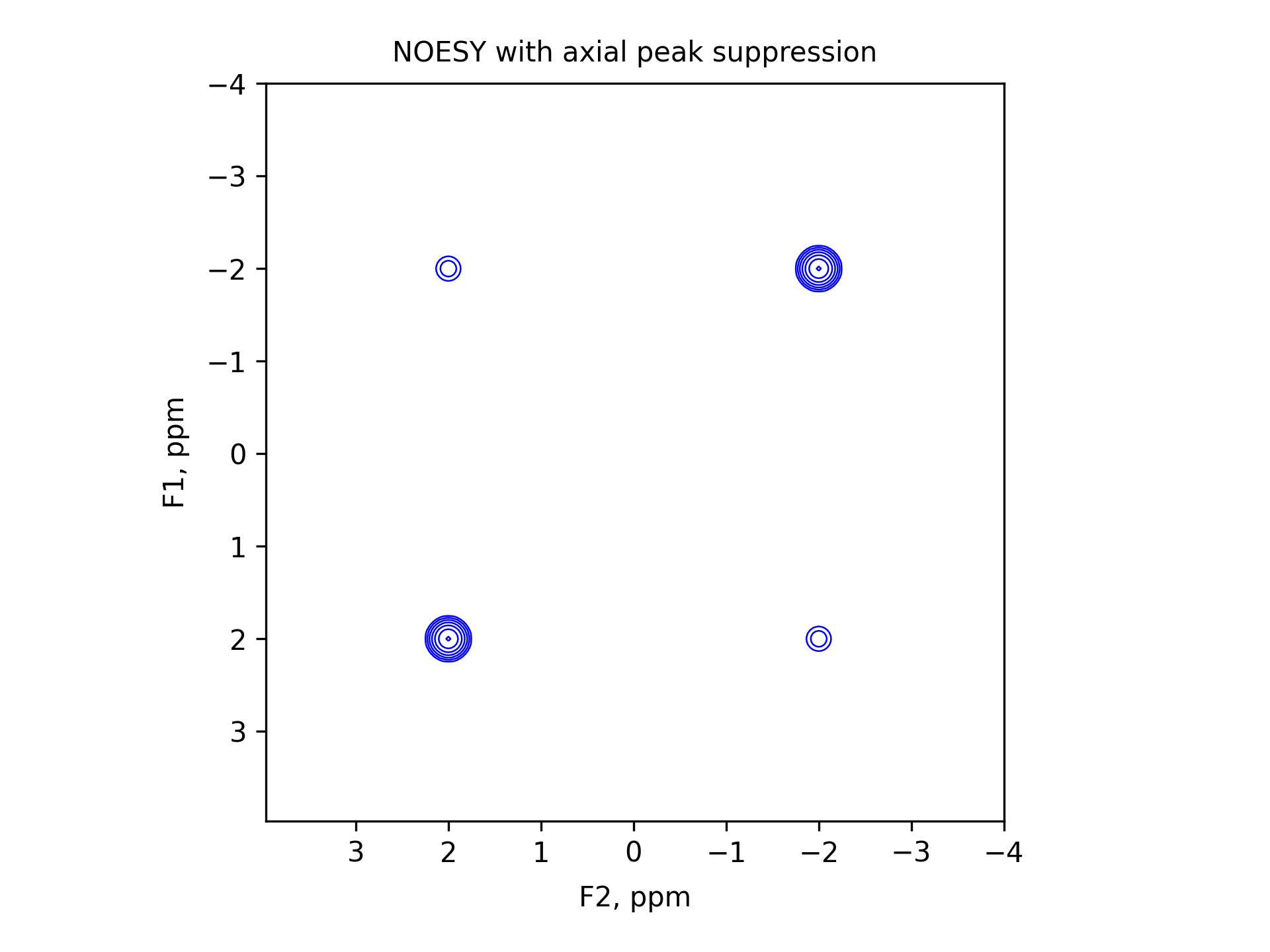
** NOESY with axial peak suppression, hypercomplex-detected **
****** The System *************************************************
spectrometer(MHz) 500
spinning_freq(kHz) *
channels H1
nuclei H1 H1
atomic_coords *
cs_isotropic -2 2 ppm
csa_parameters *
j_coupling *
quadrupole *
dip_switchboard *
csa_switchboard *
exchange_nuclei *
bond_len_nuclei *
bond_ang_nuclei *
tors_ang_nuclei *
groups_nuclei *
******* Pulse Sequence ******************************
CHN 1
timing(usec) 0.5 (250)256D1 0.5 (200000) 0.5 (250)256D2
power(kHz) 500 0 500 0 500 0
phase(deg) 90 0 -90 0 90 0
freq_offs(kHz) 0 0 0 0 0 0
phase_cycling_cos 11113333 * * * 12341234 * 12343412(RCV)
phase_cycling_sin 44442222 * * * 12341234 * 12343412(RCV)
******* Variables ************************************************
W0= 5e-4
W1a=5e-4
W1b=5e-4
W2= 2.5e-4
T1ZQ_1_2_4=0.5/W0
T1DQ_1_2_4=0.5/W2
T1SQ_1_4=0.5/W1a
T1SQ_2_4=0.5/W1b
** Alternatively, one can use RZ/RR variables to define spin-lattice relaxation:
*R1=-(W0+2*W1a+W2)
*R2=-(W0+2*W1b+W2)
*Rc=W0-W2
*RZ_1_4="I1z"
*RZ_2_4="I2z"
*RR_4=["R1 Rc; Rc R2"]
fig_title="NOESY with axial peak suppression"
******* Options **************************************************
rho0 F1z
observables F1p
EulerAngles *
n_gamma *
line_broaden(Hz) 0 0 100 100
zerofill *
FFT_dimensions 1 2 ppm
options -re -py

